[백준] 타일 문제-2

[백준] 타일 채우기, [백준] 타일 채우기3

---

풀이

타일 채우기 문제는 이전 타일 문제에서 살짝 변형이 되었다.
문제 1)은 3xN 크기의 벽을 2x1, 1x2 크기의 타일로 채우는 방법의 수를,
문제 2)는 2×N 크기의 벽을 2×1, 1×2, 1×1 크기의 타일로 채우는 방법의 수를,
구한다.
살짝 달라졌지만 방법은 똑같았다. 점화식을 찾기 위해서 먼저 규칙을 찾았다.

문제1)
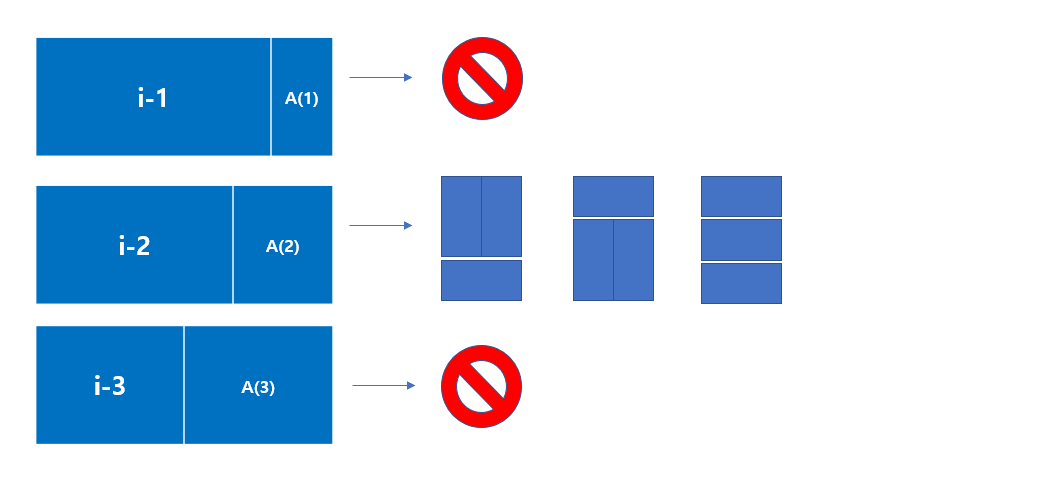
아래와 같이 그림을 보면 결과값 a(i) 일 때 모든 경우가 완성되는데,
1cm를 남겨두고 모든 경우가 완성될 경우 (i-1),
2cm를 남겨두고 모든 경우가 완성될 경우 (i-2),
3cm를 남겨두고 모든 경우가 완성될 경우 (i-3),
이라 할 때, 다음과 같이 나타낼 수 있다.

그림과 같이, 홀수 번호일 때는 경우의 수가 존재하지 않는다.
하지만 짝수 번호일 때는 경우의 수가 3개 존재한다.

이렇게 점화식을 만들 수 있지만 예외가 또 존재한다.

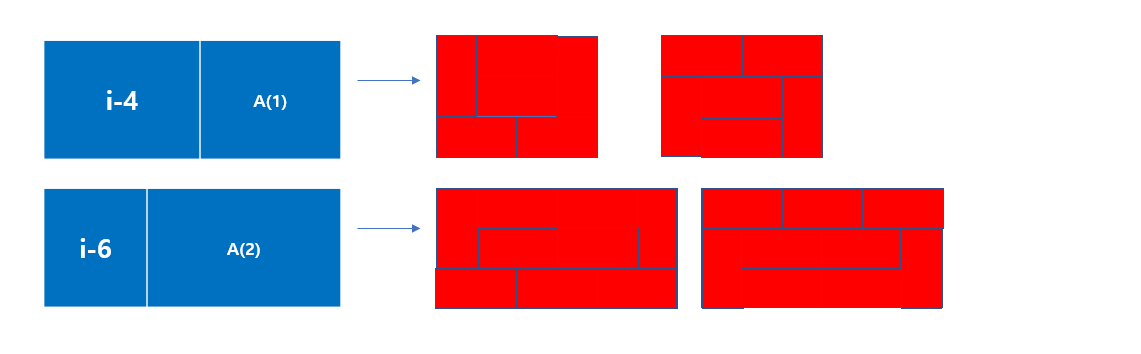
(i-4)의 경우, 3x4의 사각형에서만 만들 수 있는 사각형이,
(i-6)의 경우, 3x6의 사각형에서만 만들 수 있는 사각형이 존재한다.

즉, 2 x (a(i-4), a(i-6), a(i-8) , … , a(0)) 까지 더해줘야한다.
여기서 a(0)는 1로 현재 위치에서의 2가지 경우를 더해준다.

따라서, a(i) = 3 x a(i-2) + 2 x (a(i-4) + a(i-6) + … + a(0)) 가 된다.
(단, if i%2 == 0 일 경우만 성립한다.)

문제2)
문제 2번도 위와 같은 경우이다.
하지만 여기서는 홀수, 짝수 구별 없이 a(i-3) 부터 2가지 방법이 추가 된다.
따라서, a(i) = 2 x a(i-1) + 3 x a(i-2) + 2 x (a(i-3) + a(i-4) + … + a(0)) 가 된다.

그런데 여기서 문제는 문제2와 같은 방법으로 sum을 할 경우, 시간초과가 뜨게 된다.
(왜 그런지,, 정확한 이유는 더 공부해봐야 알 것 같다.)
그래서 새로운 저장 공간에 sum 하는 곳을 넣어준다.

2 x (a(i-3) + a(i-4) + … + a(0)) 이 부분을 새로운 공간 (메모제이션) 에 넣어 만들어주고 dp에서 필요할 때 참조할 수 있도록 한다.

# 문제1) 타일 채우기
n = int(input())
def solution(n):
    d = [0] * 31
    d[2] = 3
    for i in  range(4, n+1):
        if i % 2 == 0:
            d[i] = 3 * d[i-2] + 2 * sum(d[:(i-3)]) + 2
    return d[n]
print(solution(n))

# 문제2) 타일 채우기3
n = int(input())
def solution(n):
    d = [0] * (n+1)
    d[0:3] = [1,2,7]
    sum_d = 0
    for i in range(3, n+1):
        sum_d += d[i-3]
        d[i] = (2*d[i-1] + 3*d[i-2] + 2*sum_d)% 1000000007
    return d[n]
print(solution(n))

---

실수 및 배운 점

• 많은 수열을 고려하면서 또 다른 예외가 있는 지 항상 찾자.

• 2차 dp 이용안해도 괜찮다, sum을 만들어 다른 저장소에 메모제이션 해줄 수 있다.

• 실수했던 것은 문제2)에서 n = 1일 경우, d = [0, 0] 이 만들어지는 데,
  d[0] = 1, d[1] = 2, d[3] = 7 을 해서 error가 생겼다.
  인덱싱은 ‘참조’를 해서 그 안에 집어 넣는 것이라는 걸 알게 되었다.
  
  대신 슬라이싱을 통해 어떤 값이 들어와도 list를 extend할 수 있게 만들어줬다.
  슬라이싱은 indexing과 함께 extend도 할 수 있는 메소드라는 것을 알게 되었다.!!