[백준] 타일 문제-1

[백준] 2*n 타일, [백준] 2*n 타일2

---

풀이

타일 문제는 dp를 이용한 대표적인 문제이다. 2*n 타일 문제의 경우 2*n크기의 직사각형에 1*2, 2*1 타일을 놓는 경우, 방법의 수를
2*n 타일 문제2의 경우 2*n크기의 직사각형에 1*2, 2*1, 2*2 타일을 놓는 경우, 방법의 수를
구하는 문제다.

여느 dp와 마찬가지로 방법을 구하기 위해서는 점화식을 세워 공통된 특징을 찾아야하 한다.

문제1)
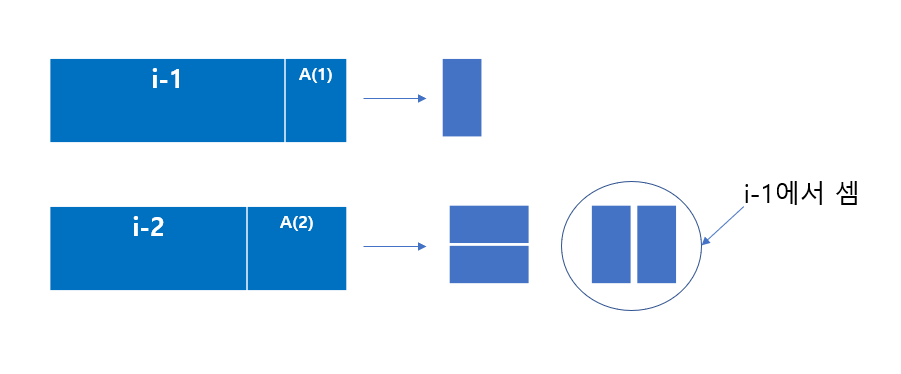
아래와 같이 그림을 보면 결과값 a(i) 일 때 모든 경우가 완성되는데,
1cm를 남겨두고 모든 경우가 완성될 경우 (i-1),
2cm를 남겨두고 모든 경우가 완성될 경우 (i-2),
를 살펴보면 다음과 같은 경우가 생긴다.

즉, i-1까지 모든 경우가 완성 됐으니 a(i-1) 일 때, a(i-1) * A(1) 을 하면 a(i)를 만들 수 있다.
마찬가지로 i-2까지 모든 경우가 완성 됐으니 a(i-2) 일 때, a(i-1) * A(2) 를 하면 a(i)를 만들 수 있다.
i-3의 경우는 i-2일 때와 i-1일 때의 조합으로 완성될 수 있으므로, 고려하지 않는다.

여기서 i-2의 경우 2*1 막대 2개를 놓을 수 있는 데, 이것은 i-1의 결과 값에 포함되고 2*1 막대 1개일 경우에 셈이 된다.
따라서, 점화식은 a(i) = a(i-1) + a(i-2) 가 된다.

이것을 코드로 짜면 아래 코드와 같다.

문제2)
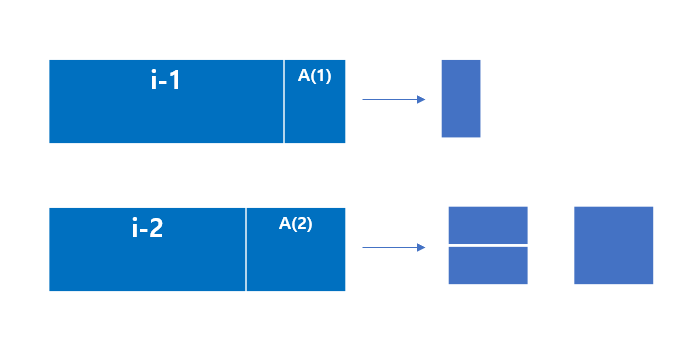
문제 2번도 위와 같은 경우이다.
하지만 여기서는 i-2의 경우 2*2 의 사각형이 추가된 것이다.
따라서, 점화식은 a(i) = a(i-1) + 2*a(i-2) 가 된다.

# 2xn 타일링

n = int(input())
def solution(n):
    d = [0] * 1001
    d[1] = 1
    d[2] = 2
    for i in range(3, n+1):
        d[i] = d[i-1] + d[i-2]
    return d[n] % 10007
print(solution(n))

# 2xn 타일링 2
n = int(input())

def solution(n):
    d = [0] * 1001
    d[1] = 1
    d[2] = 3
    for i in range(3, n+1):
        d[i] = d[i-1] + d[i-2]*2
    return d[n] % 10007
print(solution(n))

---

실수 및 배운 점

• 점화식을 만들 때는 결과값을 생각하면서 규칙성을 파악하고 만들자!