[네이버 부스트 캠프] AI-Tech - week5(2)
Linear Regression
1. Data set 내에서 Training Data와 Test Data를 명시
x_train = torch.FloatTensor([[1],[2],[3]])
y_train = torch.FloatTensor([[2],[4],[6]])
2. Hypothesis(가설) 함수를 찾기 위해 Weight, Bias 0으로 초기화
$y = Wx + b$
W = torch.zeros(1, requires_grad = True)
b = torch.zeros(1, requires_grad = True)
hypothesis = x_train * W + b
3. Compute Loss
Cost Funtion은 만들어진 Hypothesis Function과 실제 데이터 Y값의 차이의 제곱의 평균을 나타낸다.
$Cost(W, b) = \frac{1}{m}\sum_{i = 1}^{m}(H(x^{i}) - y^{i})^{2}$
위의 식을 pytorch를 이용해 나타내면 다음과 같이 한줄로 나타낼 수 있다.
cost = torch.mean((hypothesis - y_train) ** 2)
4. gradient descent
위의 Cost Function에서 값이 최소가 되는 ‘W’를 찾기 위해서는
W로 편미분 했을 때 기울기가 0에 가까운 값이 최소가 되게 된다.
위의 이론을 자세한 설명은 그 다음 번호에서 하겠습니다.
Gradient Descent 의 이론을 pytorch에서 이용할 때는 최적화가 잘된
SGD(Stochastic Gradient Descent) 를 이용한다.
SGD는 확률적 경사 하강법이라는 의미다. 본래의 Gradient Descent에서 Loss Function을 최소화하는 값을 찾기 위해 기울기의 반대방향으로 일정 크기만큼 이동하는 것을 반복한다.
여기서 Train-Set을 사용하는 것을 Batch Gradient Descent 라고 하는데, 이 경우 ‘전체’ Training Set을 이용하는 것이기 때문에 많은 계산이 필요하다. 이 방대한 양의 계산을 방지하기 위해서 확실한 답이 나올 수는 없지만 확률적 근사치로 접근하기 위해 ‘일부’ Training Set을 이용(Mini-Batch)를 사용하여 Loss Function을 계산하는 방법을 SGD라고 한다.
SGD에 대한 자세한 내용은 망나니개발자 님의 블로그 참고
optimizer = optim.SGD([W, b], lr = 0.01)
optimizer.zero_grad() # gradient 초기화
cost.backward() # gradient 계산
optimizer.step() # step() 으로 개선
이를 통해, 결과적으로 최적의 W, b를 결정한다.
5. gradient descent - 2
Gradient Descent를 자세히 설명해 보자.
-
Simplify Hypothesis Function
Hypothesis Function의 Bias를 생략하여 단순화한다.
$H(x) = Wx$
이 때의 Data는 Input = Output 으로 둔다.
x_train = torch.FloatTensor([[1], [2], [3]]) y_train = torch.FloatTensor([[1], [2], [3]])위와 같이 주어진다면, W = 1일 때, 즉, H(x) = x 일 때 정확한 모델이다.
-
Cost Funtion : MSE (Mean Squared Error)
$ cost(W) = \frac{1}{m} \sum^m_{i=1} \left( Wx^{(i)} - y^{(i)} \right)^2 $
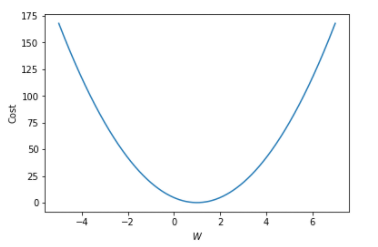
다음과 같이 나타낼 수 있다.
1에서 멀어질수록 차이는 높아지는 것을 볼 수 있다.
여기서 기울기가 가장 작을 때를 계산한다면, 최적의 W를 찾을 수 있다.$ \nabla W = \frac{\partial cost}{\partial W} = \frac{2}{m} \sum^m_{i=1} \left( Wx^{(i)} - y^{(i)} \right)x^{(i)} $
최적의 W를 찾기 위해서 W로 편미분해서 기울기를 찾는 식을 만들 수 있다.
$ W := W - \alpha \nabla W $
현재 W값과 그때의 미분값을 빼면서 W값을 업데이트 시킨다.
그리고 업데이트된 W값을 다시 cost function에 넣어 계산을 하면
W의 값이 점점 기울기의 최소값에 가깝게 된다.
여기서 $\alpha$ 는 Learning rate로, 기울기를 찾는 비율을 얼만큼씩 줄여나갈 것인가를 나타낸다.위의 식을 코드로 나타내면 다음과 같다.
gradient = torch.sum((W * x_train - y_train) * x_train) lr = 0.1 W -= lr * gradient
6. 결론 Full Code
이제 위의 식들을 합쳐서 Full Code로 나타내면, 다음과 같다.
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1)
# learning rate 설정
lr = 0.1
nb_epochs = 10
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W
# cost gradient 계산
cost = torch.mean((hypothesis - y_train) ** 2)
gradient = torch.sum((W * x_train - y_train) * x_train)
print('Epoch {:4d}/{} W: {:.3f}, Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), cost.item()
))
# cost gradient로 H(x) 개선
W -= lr * gradient
#Epoch 0/10 W: 0.000, Cost: 4.666667
#Epoch 1/10 W: 1.400, Cost: 0.746666
#Epoch 2/10 W: 0.840, Cost: 0.119467
#Epoch 3/10 W: 1.064, Cost: 0.019115
#Epoch 4/10 W: 0.974, Cost: 0.003058
#Epoch 5/10 W: 1.010, Cost: 0.000489
#Epoch 6/10 W: 0.996, Cost: 0.000078
#Epoch 7/10 W: 1.002, Cost: 0.000013
#Epoch 8/10 W: 0.999, Cost: 0.000002
#Epoch 9/10 W: 1.000, Cost: 0.000000
#Epoch 10/10 W: 1.000, Cost: 0.000000
optim 라이브러리의 SGD를 활용한다면, 다음과 같다.
# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[1], [2], [3]])
# 모델 초기화
W = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W], lr=0.15)
nb_epochs = 10
for epoch in range(nb_epochs + 1):
# H(x) 계산
hypothesis = x_train * W
# cost 계산
cost = torch.mean((hypothesis - y_train) ** 2)
print('Epoch {:4d}/{} W: {:.3f} Cost: {:.6f}'.format(
epoch, nb_epochs, W.item(), cost.item()
))
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
#Epoch 0/10 W: 0.000, Cost: 4.666667
#Epoch 1/10 W: 1.400, Cost: 0.746666
#Epoch 2/10 W: 0.840, Cost: 0.119467
#Epoch 3/10 W: 1.064, Cost: 0.019115
#Epoch 4/10 W: 0.974, Cost: 0.003058
#Epoch 5/10 W: 1.010, Cost: 0.000489
#Epoch 6/10 W: 0.996, Cost: 0.000078
#Epoch 7/10 W: 1.002, Cost: 0.000013
#Epoch 8/10 W: 0.999, Cost: 0.000002
#Epoch 9/10 W: 1.000, Cost: 0.000000
#Epoch 10/10 W: 1.000, Cost: 0.000000