[네이버 부스트 캠프] AI-Tech - Lv3 모델 경량화(2)
학습 기록 - 좋은 모델과 파라미터 찾기 : AutoML 이론
Conventional DL pipeline이 어떤 문제를 해결? 목적?
Configuration의 특성?, 경량화 관점에서 AutoML이 어떤 의미를 가지는지?
AutoML Pipeline 구현 & 한계점, 현실적인 접근?
Overview
Conventional DL Training Pipeline
“Data Engineering”이라 하면,
우리가 이전에 했듯이 데이터를 정제하고 전처리를 거친 후,
Feature Engineering을 진행한 후에, (주어진 데이터로 예측 모델의 문제를 잘 표현하는 features로 변형시키는 과정)
적합한 모델을 선정해서 (ML Algorithm) 적합한 Hyperparameters를 선정합니다.

위와 같은 Data Engineering을 거친 후, 적합한 모델의 Architecture와 Hyperparameter (좋은 Configuration) 를 위해서 Train & Evalutation을 반복하게 됩니다.
여기서 이 과정은 사람이 끊임없이 반복하게 됩니다.
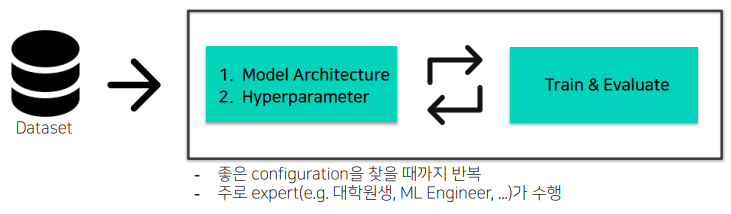
Objectives of AutoML
위와 같은 과정들은 고객의 요구사항에 의해 새로운 데이터가 들어오거나 또 다른 예측 output을 내고 싶다면, 새롭게 tuning을 하게 됩니다.
여기서 사람들이 작업해야하는 과정을 빼내고자 하는 것이 Automated Machine Learning(AutoML) 의 목표입니다.

AutoML의 문제 정의
HyperParmeter Sample에 대해서 Algorithm, Data Train, Data Valid가 정의되어 있을 때, Loss가 가장 낮은 Hyperparameter를 정의해주는 것

Properties of configurations in DL
DL model Configuration (Architecture, Hyperparameter)의 특징
-
주요 타입 구분
- Categorical
- ex) optim : (Adam, AdamW, SGD) module : (Conv, BottleNeck, Residual block, ..)
- Continuous
- ex) learning rate, regularizer param, …
- Integer
- ex) batch_size, epochs, ..
- Categorical
-
⭐Conditional⭐한 Configuration에 따라 Search space가 달라질 수 있습니다.
- Optimizer의 sample(e.g.SGD,Adam등등)에 따라서 optimizer parameter의 종류, search space도 달라짐
(e.g, optimizer에 따른 learning rate range 차이, SGD:momentum, Adam:alpha,beta1,beta2,..등등) - Module의 sample (e.g.VanillaConv, BottleNeck, InvertedResidual 등등)에 따라서 해당 module의 parameter의 종류,search space도 달라짐
- Optimizer의 sample(e.g.SGD,Adam등등)에 따라서 optimizer parameter의 종류, search space도 달라짐
모델 경량화 관점에서의 AutoML
모델을 경량화하는 것은 두가지 관점이 존재합니다.
기존 모델 경량화 vs 새로운 경량 모델 Search
- 기존 모델 경량화 : Pruning, Tensor decomposition, … -> 이러한 기법들은 후처리가 있어야 성능이 나옵니다.
- 새로운 경량 모델 Search : NAS(Neural Architecture Search), Auto
Basic Concept
AutoML Pipeline
일반적인 AutoML Pipeline
Configuration : Backbone, hyperparam 모두 포괄
Evaluate Objective : 어떤 Task에 따라 다르다? -> 성능, 속도 or 성능 등등 Task마다 원하는 수치 값을 설정해준다.
Blackbox objective : 평가한 Objective값을 가지고 평가 지표를 최대로 만드는 람다를 찾는 것
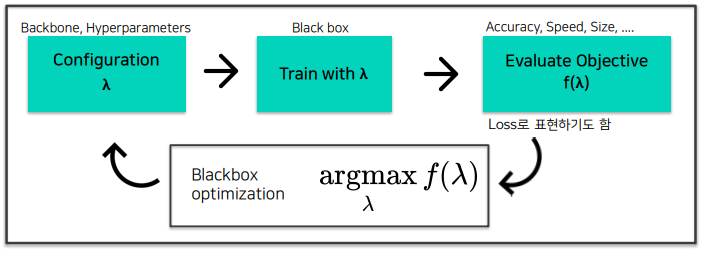
AutoML Pipeline 예시 : Bayesian Optimization (BO)
Blackbox objective : Surrogate Function -> Acquisition Function
Surrogate Function : $f(\lambda)$ 를 예측하는 Regression 모델
Acquisition Function : 다음 $\lambda$ 를 시도하는 함수
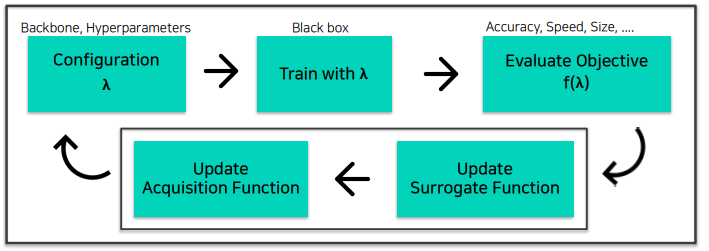
Bayesian Optimization (with Gaussian Process Regression)
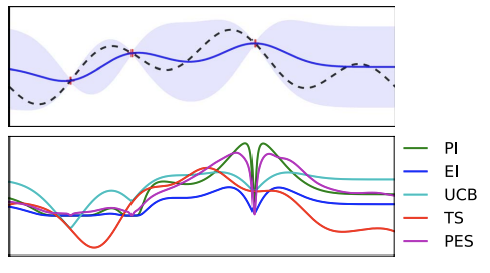
Surrogate Function과 Acquisition Function을 자세하게 살펴보면,
3번의 objective 계산 후, point가 업데이트 되는 것을 볼 수 있습니다.
point가 업데이트 됨에 따라 Surrogate model이 업데이트 됩니다. 그에 따라, 점선과 보라색 영역이 줄어들면서 좀 더 정밀해집니다.
Acquisition function은 다음 $\lambda$ 를 추천해주는 함수가 업데이트 됩니다.
위와 같은 과정을 반복합니다.
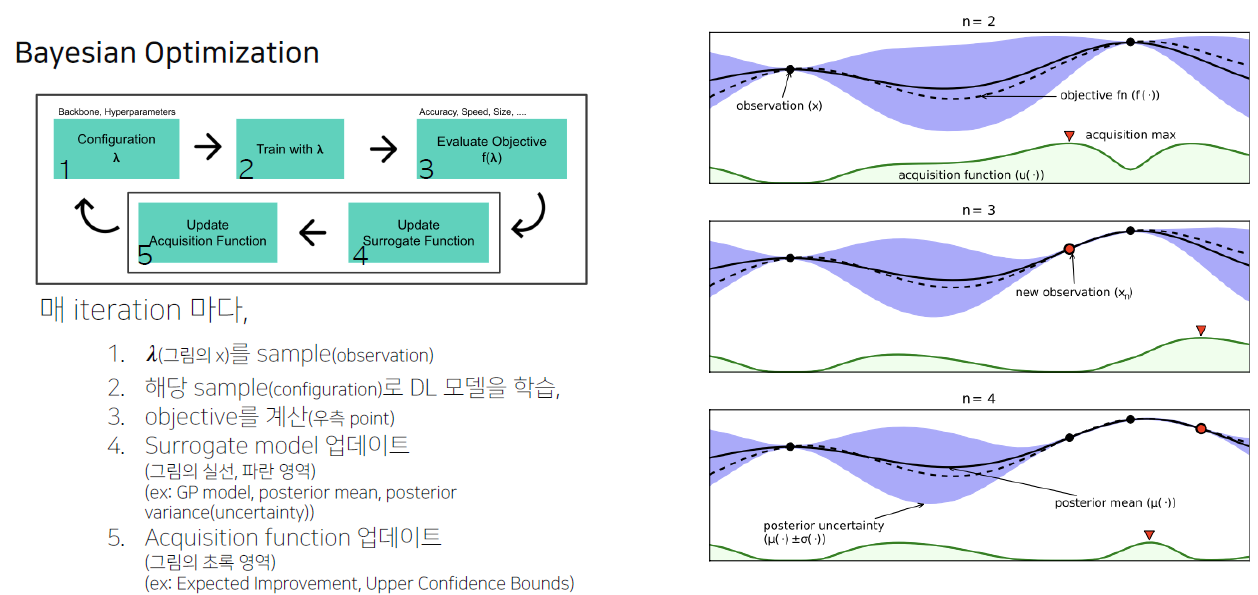
Surrrogate model은 적절한 관계성을 가지는 f(λ) 을 찾아주는 것
Acquisition Function은 적절한 관계성 속에서 가장 적절한 위치를 찾아주는 것
Bayesian Optimization (with Gaussian Process Regression) - Surrogate Model
간단 설명 : Gaussian Process Regression
-
일반적인 Regression task : “Estimate the function f fits the data the most closely”
Set of train data: (X, Y), Set of the test data : (X, Y), $Y \approx f(X)+e$ -
우리가 알고자 하는 특정 위치의 Y* 값은 우리가 알고 있는 X, Y, X* 들과 (positive건, negative건) 연관이 있지 않을까?
-> X, Y, X* 값으로부터 Y* 를 추정, 연관에 대한 표현은 Kernel 함수 K로 표현 -
f(x)를 “Possible output of the function f at input x”인 “Random variable”로 보고, 각 r.v.들이 Multivariate Gaussian distribution 관계에 있다고 가정
= 함수들의 분포를 정의하고, 이 분포가 Multivariate Gaussian distribution을 따른다 가정
= 함수 f가 Gaussian process를 따른다.식의 표현은 아래와 같습니다.
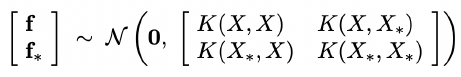
-
결국, 위 식의 표현은 알고자 하는 값(test)과 알고있는 값(train)의 관계를 Multivariate Gaussian이라고 정의한 것이다.
-
Gaussian Identities (Gaussian의 marginal, conditional도 Gaussian)
위와 같은 정의를 따를 때, Multivariate Gaussian의 marginal, conditional한 값도 Gaussian 분포를 따를 수 있다.
이 식의 의미는 관계가 정의가 된다면 f와 데이터가 주어졌을 때, f*의 Conditional 분포를 정의해줄 수 있음을 의미합니다.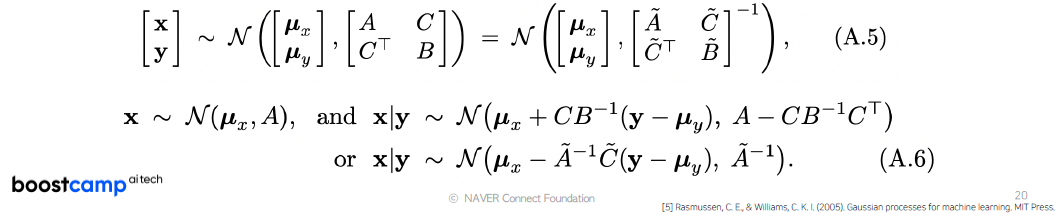
그림으로 보충 설명을 하자면, Multivariate Gaussian의 관계를 가질 때, 어느 위치에서 보더라도 모두 Gaussian Distribution을 이룬다.
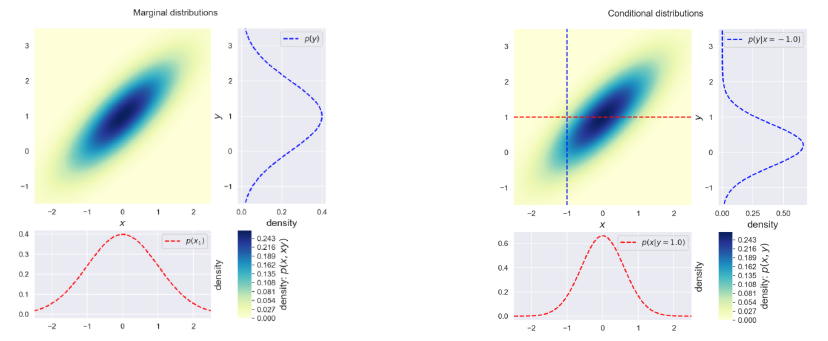
결론적으로, 이전에 설명했던 f와 f* 사이에 관계를 다음과 같이 Multivariate Gaussian으로 정의 된다면,
X, f, X* (X* : 다음 데이터) 만으로 f|X의 분포를 평균, 분산으로 정의를 내릴 수 있습니다.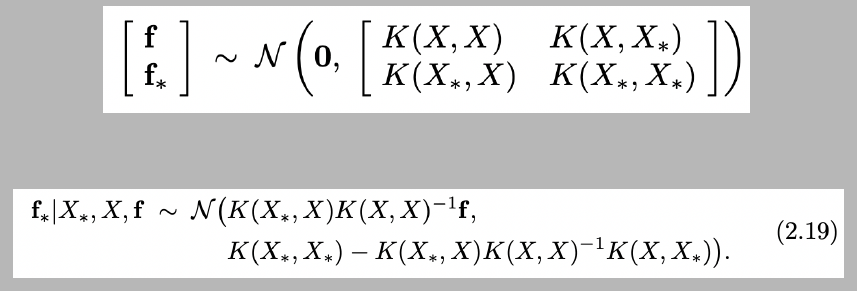
-
Surrogate Model(Function): $f(\lambda)$ 의 Regression model
-
정의 : Objective $f(\lambda)$ 값을 예측하는 모델
지금까지 관측된 $f(\lambda)$ 가 있을 때, 새로운 $\lambda^{ * }$ 에 대한 objective $f(\lambda^{ * })$ 값은 얼마일까? -
Objective를 estimate하는 surrogate model을 학습, 다음 좋은 $(\lambda)$ 를 선택하는 기준으로 사용
-
대표적인 Surrogate model로는 Gaussian Process Regression(GPR) Model
(Mean: 예측 f값, Var: uncertainty)
-
Bayesian Optimization (with Gaussian Process Regression) - Acquisition Function
Acquisition Function : 다음은 어디를 trial하면 좋을까?
- Surrogate model의 output으로부터, 다음 시도해보면 좋을 $\lambda$ 를 계산하는 함수
- Exploration vs Exploitation
(“불확실한 지점 vs 알고있는 가장 좋은 곳”의 trade off) 이 2개를 huristic하게 (balancing) 찾아주는 것 - Acquisition function의 max 지점을 다음 iter에서 trial
-
ex) Upper Confidence Bound(UCB)
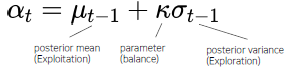
Bayesian Optimization (with Tree-structured Parzen Estiamtor)
Tree-structured Parzen Estimator(TPE)
- GP (Gaussian process)의 약점:
- High-dim(O(N**3))
- Conditional, continuous/discrete 파라미터들의 혼재시 적용이 어려움 -> 다른 테크닉들의 적용이 필요
-
TPE : GPR( $p(f \mid \lambda)$ )와 다르게 $p(\lambda \mid f)$ 와 $p(\lambda)$ 를 계산
-
TPE를 통한 다음 step의 $\lambda$ 계산 방법
-
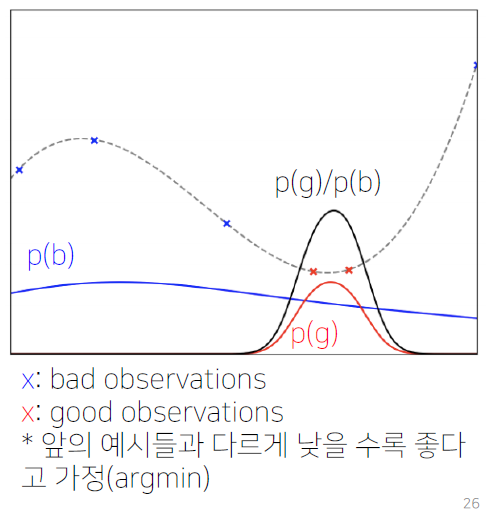
현재까지의 observation들을 특정 quantile(inverse CDF)로 구분 (ex, 전체 중 75% bad, 25% good)
-
KDE(Kernel density estimation)으로 good observations 분포(p(g)), bad observations의 분포(p(b))를 각각 추정
-
p(g)/p(b)은 EI(Expected Improvement, acquisition function 중 하나)에 비례하므로([6]), 높은 값을 가지는 𝝀를 다음 step으로 설정
-> 이 과정들을 통해서 Surrogate model & Acquisition function의 과정을 동시 수행 가능
-
Tree-structured Parzen Estimator(TPE) : EI 증명 (EI가 왜 비례하는가?)
- Likelihood를 Quantile로 구분되는 두 함수로 정의
-
증명에 대한 수식
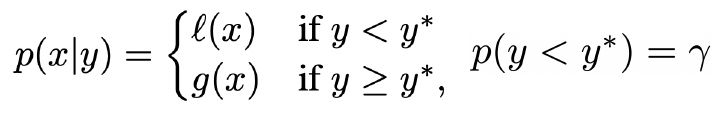

-> g분의 l에 비례한다.
위의 수식을 의미론적으로 보자면,
l(x)(좋았던 관측 분포), g(x)(안좋았던 관측 분포) 이라 할 때,
l(x)/g(x)가 가장 높은 지점을 탐색하는 것은 l(x)가 높은 쪽을 선호하되, g(x)가 낮은 곳도, 즉, 안좋은지 알 수 없는 것도 찾아보자는 의미
Further Studies
AutoML의 한계점과 현실적인 접근 방법에 대해서 알아보면?
-
하나의 iter도 굉장히 오래 걸리는 단점이 존재.
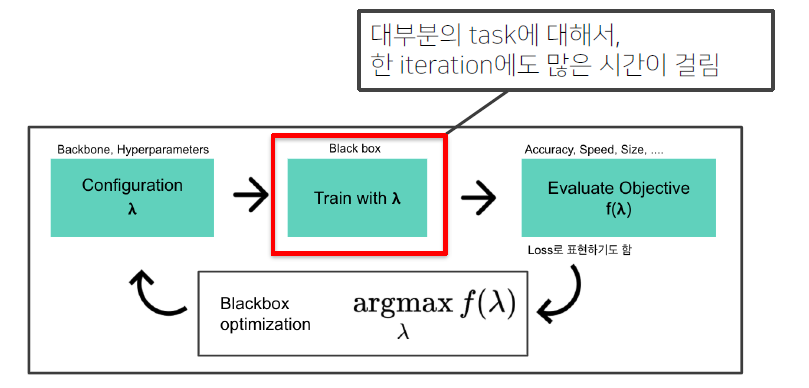
연구가 활발하게 진행되고 있다!
- DL에서의 AutoML은 Scalability 이슈가 더욱 대두됨
- 주요 키워드
- Hyperparameter GD (탐색과 학습을 동시에)
- Meto-learning(Auto “AutoML”)
- Multi-fidelity optimization -> 시간 줄이기 위한 다양한 방법
- Data의 subset만을 활용
- 적은 epoch
- RL을 활용한 적은 trial (강화학습)
- Image Downsampling
절충안 -> 충분히 가능
- 어느 정도의 prior를 개입, 적은 search space를 잡고,
- 적지만, 대표성을 띄는 좋은 subset 데이터를 정하고(+ n-fold Cross Validation 등의 테크닉)
- 학습 과정의 profile을 보고 early terminate하는 기법 적용
(ASHA Scheduler, BOHB(Bayesian Optimization & Hyperband))
등등의 방법으로 “충분히 좋은” configuration을 찾을 수 있습니다.
