Hyuns Kim

Hyuns Kim

Learn, Run 👨‍💻🏃‍♂️

[네이버 부스트 캠프] AI-Tech-re - week2(1)

학습기록 - 6

오늘 한 일

  • 딥러닝 기본 용어 설명 & 뉴럴 네트워크
  • 필수 과제 1
  • 피어세션 ) 딥러닝개요, 정규표현식 & 문자열 알고리즘 (KMP 알고리즘- 접두사와 접미사의 최대 일치 길이 찾아주는 역할, 보이어 무어, 라빈 카프)

1. 강의 복습 내용

Deep Learning 개요

  • Key Components of Deep Learning

    1. data
    2. model
    3. loss
    4. algorithm

  • loss

    1. Loss
    2. classification
    3. probabilistic

  • optimization Algorithm

    • SGD, Momentum, NAG, Adagrad, Adadelta, Rmsprop

  • Model

    • Alexnet, GoogLeNet, ResNet, DenseNet, LSTM, Deep AutoEncoders, GAN

Deep Learning 관련 정리

Neural Network : Neural Network는 뇌에 있는 뉴런을 본따서 만든 학습 알고리즘을 말한다. 뉴럴 네트워크는 affine transformation 에 의해 어떤 벡터 공간을 다른 벡터 공간으로 넘겨주는 알고리즘이 쌓여있는 것과 같다.

what ? 우리가 Deep Learning에서 하고자 하는 목적은 결국, ‘예측 모델”을 찾는 것이다.
how ? 여기서 예측 모델에는 각각 적당한 Parameter를 가지고 있다. 그 Parameter를 예측하기 위해서 임의의 Hypothesis 함수를 만들고 그 함수값과 실제값의 차이 즉, Loss를 파악한다. 그리고 Loss를 최소로 만드는 Parameter 값을 다시 업데이트 시켜주면서 적절한 모델을 만들어낸다.

  • Linear Neural Networks (hypothsis model : linear function)

    데이터(D)가 주어지고 Model을 선형적으로 간다고 가정했을 때 (hypothesis),
    Loss 값은 MSE(Mean Square Error) 에 따라 나타낼 수 있다.

    Data: $\mathcal{D}={\left(x_{i}, y_{i}\right)}_{i=1}^{N}$

    Model: $\hat{y}=w x+b$

    Loss: $\operatorname{loss} \beta=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2}$

    다음과 같이 Loss를 나타낼 때, Parameter (W, b)를 최소로 만드려면 Partial Derivatives (편미분) 를 이용한다.

    \[\begin{aligned} \frac{\partial \operatorname{loss}}{\partial w} &=\frac{\partial}{\partial w} \frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} \\ &=\frac{\partial}{\partial w} \frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-w x_{i}-b\right)^{2} \\ &=-\frac{1}{N} \sum_{i=1}^{N}-2\left(y_{i}-w x_{i}-b\right) x_{i} \end{aligned}\]

    b의 경우도 같은 방법으로 해주면, 다음과 같이 나타낼 수 있다.

    $\begin{aligned} \frac{\partial \operatorname{loss}}{\partial b} &= -\frac{1}{N} \sum_{i=1}^{N}-2\left(y_{i}-w x_{i}-b\right) \end{aligned}$

    이제 Parameter(w, b)를 업데이트하기 위해서 Gradient Descent에 의해 다음과 같은 식이 나온다.

    $w = w-\eta \frac{\partial \operatorname{loss}}{\partial w}$
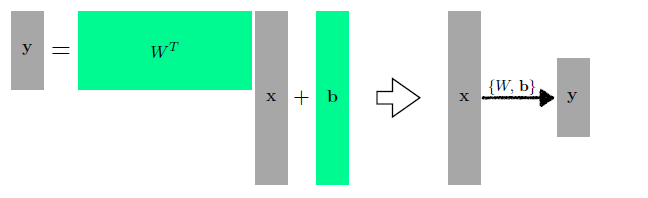
    $b ~= b-\eta \frac{\partial \operatorname{loss}}{\partial b}$

    이제부터는 Parameter가 여러개 일 때, (multi-dimensional) 모델을 다뤄보자면, 여기서는 행렬을 이용해서 나타낼 수 있다. (affine matrix) 두 차원의 선형 변환을 찾는 것이다.

    s1

    여기서 우리는 위와 같은 그림을 토대로 행렬을 쌓아서 Deep Learning을 할 수 있도록 한다.
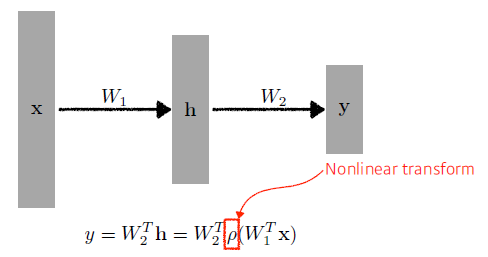
    Deep Learning을 할 때는 다음과 같이 W1을 통해 H (hidden layer)가 나오고, 그 다음 W2를 통해 y (output)이 나오게 된다.

    $\left.h=\right.W_{1}^{T}\mathrm{x}$
    $\left.y=W_{2}^{T} \mathbf{h}=\right.W_{2}^{T} W_{1}^{T} \mathrm{x}$

    하지만 이렇게 쌓는다면, $W_{2}^{T} W_{1}^{T}$ 은 차원의 곱으로 한 단짜리 Nerual Network와 다를게 없다. 이를 방지하기 위해 아래와 같이 선형 결합 후 비선형 함수인 $\rho$ (activation function) 를 넣어서 많은 표현력을 갖게 해준다.
    (여기서 activation function에는 ReLu, Sigmoid, tanh)

    s2

    위와 같은 식에 의해 만들어진 Net을 통해 만들어진 결과값 즉, 예측값을 y_hat 이라 한다면, loss function은 크게 모델에 따라 3가지로 나타낼 수 있다.

    1. Regression Task $\mathrm{MSE}=\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D} (y_{i}^{(d)} - \hat{y}_{i}^{(d)})^2$

    2. Classification Task $\mathrm{CE}=-\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D} y_{i}^{(d)} \log \hat{y}_{i}^{(d)}$

    3. Probabilistic Task $\mathrm{MLE}=\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D} \log \mathcal{N}\left(y_{i}^{(d)} ; \hat{y}_{i}^{(d)}, 1\right) \quad(=\mathrm{MSE})$

2. 고민 내용, 결과 (과제 수행 과정, 결과물 정리)

  1. 필수 과제 : mlp
    • MNIST 데이터 셋을 가져와서 train set, test set으로 분리한다.
    • MLP 모델 객체화 (nn.Module, xdim = 784 -> hdim = 256 -> ydim = 10)

    • sforward path of the mlp model :
      random x값 파이토치화 x_numpy -> x_torch, 파이토치에서 돌리기 위해서는 내가 활용하는 gpu device를 넣어야한다.
      torch화 된 x값을 forward propagation을 통해 y_torch를 만들고 tensor -> numpy 화

    • check parameter : lin_1 과 lin_2 shape의 weight과 bias의 변화를 보여줌

    • Evaluation Function : 위의 검사들이 다 끝났으면, MNIST 데이터의 예측 모델을 만들고 accuracy 확인

    • Train : epoch 별 모델 손실도, 예측도 확인

3. 피어세션 정리

[ 2021년 8월 9일 회의록 ]

✅오늘의 피어세션 (모더레이터: 양준혁)

  1. 강의 요약 발표 진행
    • 내용: DL 개요 및 NN 정리 -> MLE, MSE, CE 관련 질문
  2. 알고리즘 스터디
    • 내용 : 정규표현식 & 문자열 알고리즘 (KMP 알고리즘- 접두사와 접미사의 최대 일치 길이 찾아주는 역할, 보이어 무어, 라빈 카프)
  3. 주간 피어세션 일정 조율
    • 특강날짜의 피어세션 진행
    • 시각화 강의 관련 일정 조율
    • 금요일 피어세션 시간 조율 > 알고리즘 부분 제외

4. 학습 회고

  • Deep Learning 에 대한 개요를 통해 그동안 어렵게 배웠던 모델의 이해를 빠르게 알 수 있었다.

  • 피어세션 정규표현식에 대해 처음 알게 되었고, 새롭게 공부를 할 수 있었다.

  • 계획을 세웠지만, 확실한 결정을 서지 못해 고생했다. 내가 했던 계획은 확실하게 지키고 애매하게 알고 넘어가지 말자.

참고